
Fig (4.11): Circle in isometric projection
4.7a. Four Centre Approximation:
In Fig (4.12) one rectangle ABCD is enclosing the circle. Take the mid point E, F, G & H of lines AB, BC, CD, DA. Now draw the rectangle ABCD in isometric axes and also locate the points E, F, G & H as the mid points of the sides of rectangle. Now draw lines AG & AF, CH & CE. Lines AG & CH are intersecting at M while lines CE & AF are intersecting at N. now we have got the four center points to draw an ellipse i.e. A, M, C & N.
a) By taking A as center and AG as radius draw the arc FG.
b) By taking M as center and MH as radius draw the arc GH.
c) By taking C as center and CE as radius draw the arc EH.By taking N as center and NF as radius draw the arc EF.
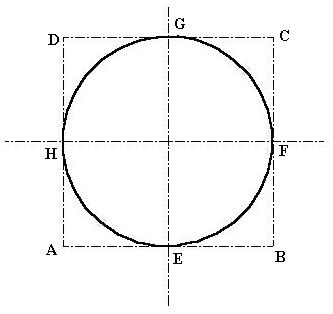
Fig (4.12): Rectangle ABCD enclosing the Circle

Fig (4.13): Method to draw the Isometric projection of Circle on the top face of Cube

Fig (4.14): Isometric Projection of Circle on the side faces of cube
4.8 Isometric projection of solids:
An object having length, width and height is generally said as solid. Pyramids, prisms, cylinder, cone, cube, sphere and frustums of these are all solids.
4.8a Prisms:
A prism has similar top face and bottom face (base). If the axis of prism is perpendicular to its base it is called a right prism. And when all its faces are rectangles of same dimension then it is said to be regular prism. The prism is generally known by its base, i.e. if the base of prism is triangle it is called as triangular prism, and if is hexagon then it is called hexagonal prism and so on. The boxing method can be used to draw isometric projections of all prisms.
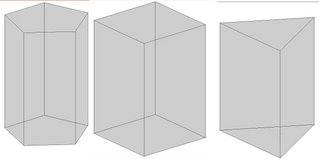
Fig (4.15): Different types of Prisms. A) Triangular Prism B) Rectangular Prism C) Pentagonal Prism
4.8a(1) Isometric Projection of Triangular Prism:
For making isometric projection of triangular prism, enclose the base of prism i.e. triangle in a rectangle ABCD and locate the contact point of triangle E on line CD as shown in fig (4.17A). Now draw a box (dimensions a, b, & c as Length, width & Height respectively) in vertical position in isometric projection as shown in fig (4.17B). On the edges CD & C’D’ of Box locate E & E’. Now draw triangles on the bottom & top faces of Box by making AE, BE, A’E’ & B’E’. Now Join E & E’ and complete the isometric projection of Triangular Prism.

Fig (4.16): Pictorial drawing of Triangular prism with dimensions

Fig (4.17): Method to draw isometric projection of Triangular prism. (A) Triangle enclosed in Rectangle ABCD, (B) Triangular Prism enclosed by Box.
In the same way triangular prism can be draw in other isometric axis as shown in fig (4.19).

Fig (4.18): Pictorial drawing of Triangular prism in other isometric axis
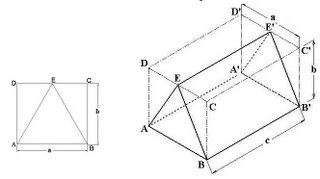
Fig (4.19): Method to draw isometric projection of Triangular prism in other isometric axis. (A) Triangle enclosed in Rectangle ABCD, (B) Triangular Prism enclosed by Box.